Vektoren

Rechnen mit Vektoren in Koordinatendarstellung

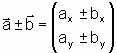
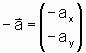
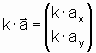
Die Addition und Subtraktion von Vektoren sowie die Multiplikation mit einer Zahl erfolgen koordinatenweise:

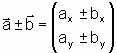
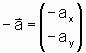
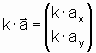
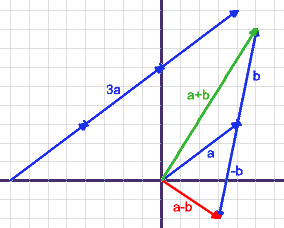
Beispiel:
a = , b =
a + b =
a − b =
3·a =

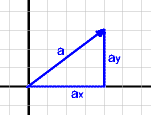Den Betrag eines Vektors berechnet man mit Hilfe des Satzes von Pythagoras:

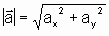
Beispiel:
Von einem Parallelogramm kennt man die Eckpunkte A(1/0), B(5/2) und D(−2/3). Berechne den fehlenden Eckpunkt und den Umfang!
Wir berechnen die Seitenvektoren: AB = , AD =
AB = DC, wir müssen also den Vektor AB von D aus auftragen:
, C hat also die Koordinaten C(2/5).
(Wir hätten auch AD von B aus auftragen können.)
Die Seitenlängen sind a = = 4,47 und b = = 4,24.
Der Umfang beträgt u = 2·(a + b) = 17,43.

Zwei Vektoren sind parallel, wenn der eine ein Vielfaches des anderen ist.

Beispiel: u = , v =
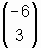
v = -3·u ⇒ u // v

Im Raum rechnet man analog mit 3 Koordinaten.

Zu einem gegebenen Vektor in der Ebene findet man einen Normalvektor, indem man die Koordinaten vertauscht und bei einer Koordinate das Vorzeichen ändert:

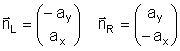
n_L erhält man, wenn man a um 90° nach links dreht, n_R bei Drehung von a um 90° nach rechts. (Im Raum gibt es zu einem gegebenen Vektor unendlich viele Normalvektoren, daher geben wir dafür keine Formel an.)

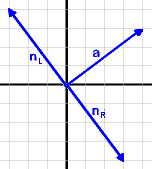
Beispiel: a = ⇒ n_L = , n_R =

Den Mittelpunkt einer Strecke AB erhält man, indem man z.B. von A aus die Hälfte des Vektors AB aufträgt:
M_AB = A + ½·AB = A + ½·(B − A) = ½·A + ½·B
Wir erhalten daher die leicht zu merkende Formel:

(Jetzt kannst du den Abschnitt "Parameterform der Geradengleichung" durchnehmen.)

Das Skalarprodukt zweier Vektoren

Es ist auch möglich, eine Art Vektormultiplikation zu definieren - allerdings ist das Produkt ein Skalar (eine Zahl).
Wir bezeichnen mit b_a die Normalprojektion des Vektors b auf den Vektor a. Dann definiert man das Skalarprodukt a·b folgendermaßen:

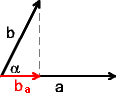
a·b = |a|·|b_a|, wenn a und b_a die gleiche Richtung haben
a·b = −|a|·|b_a|, wenn a und b_a entgegengesetzte Richtungen haben.

Anders ausgedrückt: Schließen die Vektoren a und b den Winkel α ein, so ist
a·b = |a|·|b|·cos(α)     (*)

Sind a und b parallel, so ist a·b = |a|·|b|. (Sonderfall: a·a = |a|².)
Stehen a und b normal aufeinander, so ist a·b = 0.

Im Speziellen gilt für die Basisvektoren e_x und e_y:
e_x·e_x = e_y·e_y = 1, e_x·e_y = 0.

Man kann zeigen:
Es gilt das Kommutativgesetz: a·b = b·a,
das Assoziativgesetz: (k·a)·b = k·(a·b)
und das Distributivgesetz: a·(b + c) = a·b + a·c

Damit können wir das Skalarprodukt zweier Vektoren, die in Koordinatendarstellung gegeben sind, folgendermaßen berechnen:
= (a_x·e_x + a_y·e_y)·(b_x·e_x + b_y·e_y) = a_xb_x·e_x·e_x + a_yb_x·e_y·e_x + a_xb_y·e_x·e_y + a_yb_y·e_y·e_y = a_xb_x + a_yb_y

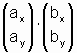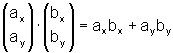
Aus der Gleichung (*) können wir jetzt den Winkel zwischen zwei Vektoren berechnen:

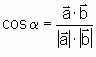
Im Raum rechnet man analog mit 3 Koordinaten.

Übungen

Zu diesem Thema gibt es einige Tests auf mathe online:
Vektoren erkennen (http://www.mathe-online.at/tests/vect1/erkennen.html)
Vektoraddition (http://www.mathe-online.at/tests/vect1/va.html)
Vektorsubtraktion (http://www.mathe-online.at/tests/vect1/differenz.html)
Skalarprodukt (http://www.mathe-online.at/tests/vect2/skalarprodukt.html)