Vektoren
Einführung
Begriffe aus der Physik:
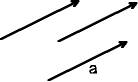 Ein Vektor ist eine gerichtete Größe (Kraft, Geschwindigkeit ... ).
Er kann durch einen Pfeil dargestellt werden (Repräsentant des Vektors).
Ein Vektor ist eine gerichtete Größe (Kraft, Geschwindigkeit ... ).
Er kann durch einen Pfeil dargestellt werden (Repräsentant des Vektors).
Die Länge des Pfeils bezeichnet man als Betrag des Vektors.
Alle gleichlangen, parallelen und gleichgerichteten Pfeile gehören zum selben Vektor.
Ein Skalar ist eine ungerichtete Größe (eine Zahl).
Man bezeichnet Vektoren üblicherweise mit Kleinbuchstaben, mit darübergestelltem Pfeil:
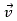 oder fett: v.
oder fett: v.
(Ich werde Vektoren der Einfachheit halber im Folgenden meist fett schreiben.)
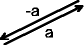 Der zu a entgegengesetzte Vektor −a heißt Gegenvektor von a.
Der zu a entgegengesetzte Vektor −a heißt Gegenvektor von a.
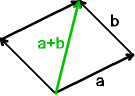 Zwei Vektoren werden addiert, indem man ihre Repräsentanten "aneinanderhängt".
Aus dem dargestellten Parallelogramm ergibt sich:
Zwei Vektoren werden addiert, indem man ihre Repräsentanten "aneinanderhängt".
Aus dem dargestellten Parallelogramm ergibt sich:
a + b = b + a
Die Summe aus einem Vektor und seinem Gegenvektor ist der Nullvektor.
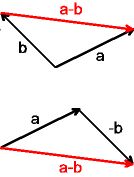 Zwei Vektoren werden subtrahiert, indem man
Zwei Vektoren werden subtrahiert, indem man
- b auf a ergänzt ("b plus wieviel ist a?") oder
- −b zu a addiert.
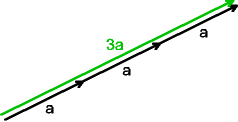 Ein Vektor wird mit einem Skalar k multipliziert, indem man ihn um den Faktor k
streckt bzw. staucht.
Ein Vektor wird mit einem Skalar k multipliziert, indem man ihn um den Faktor k
streckt bzw. staucht.
Der Vektor k·a ist parallel zu a und
- gleich orientiert, wenn k > 0
- entgegengesetzt orientiert, wenn k < 0
Zwei Vektoren sind genau dann parallel, wenn der eine das k-fache des anderen ist.
Einen Vektor der Form k·a + m·b bezeichnet man als
Linearkombination der Vektoren a und b.
Koordinatendarstellung von Vektoren in der Ebene
Seien ex, ey zwei Einheitsvektoren (Vektoren mit der Länge 1)
in Richtung der Koordinatenachsen. Dann kann man jeden Vektor der Ebene als Linearkombination
von ex und ey darstellen.
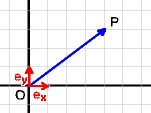
Betrachten wir z.B. den Vektor vom
Koordinatenursprung zum Punkt P(4/3) (den sogenannten Ortsvektor von P), so können wir schreiben:
OP = 4·ex + 3·ey
oder einfacher
OP = 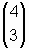
Allgemein: a = ax·ex + ay·ey
= 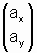
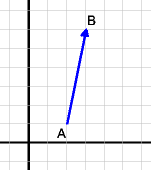 Sind Anfangs- und Endpunkt des Vektors bekannt, so gilt:
Sind Anfangs- und Endpunkt des Vektors bekannt, so gilt:
Vektor = Endpunkt - Anfangspunkt
Beispiel: A(2/1), B(3/6):
AB = 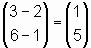
(Da alle Repräsentanten des Vektors dieselbe Koordinatendarstellung haben, kann man von den
Koordinaten des Vektors sprechen.)
Soll ein Vektor von einem gegebenen Anfangspunkt aus aufgetragen werden, so gilt:
Anfangspunkt + Vektor = Endpunkt
Beispiel: Trage den Vektor a = 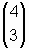 vom Punkt C(−-2/3) aus auf!
vom Punkt C(−-2/3) aus auf!
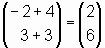 , der Endpunkt hat daher die Koordinaten D(2/6).
, der Endpunkt hat daher die Koordinaten D(2/6).
Koordinatendarstellung von Vektoren im Raum
Im Raum gibt es 3 Koordinatenachsen. Wir können daher jeden Vektor als Linearkombination
von 3 Einheitsvektoren ex, ey und ez darstellen, z.B.:
4·ex + 3·ey − 2·ez =

Anmerkung: Man kann Vektoren auch von Anfang an als geordnete Zahlenpaare bzw. Zahlentripel
definieren. Diese Definition kann man auf geordnete n-Tupel erweitern; man erhält dann Vektoren im
(nicht mehr anschaulich vorstellbaren) n-dimensionalen Raum.
 Ein Vektor ist eine gerichtete Größe (Kraft, Geschwindigkeit ... ).
Er kann durch einen Pfeil dargestellt werden (Repräsentant des Vektors).
Ein Vektor ist eine gerichtete Größe (Kraft, Geschwindigkeit ... ).
Er kann durch einen Pfeil dargestellt werden (Repräsentant des Vektors).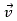 oder fett: v.
oder fett: v. 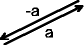 Der zu a entgegengesetzte Vektor −a heißt Gegenvektor von a.
Der zu a entgegengesetzte Vektor −a heißt Gegenvektor von a. Zwei Vektoren werden addiert, indem man ihre Repräsentanten "aneinanderhängt".
Aus dem dargestellten Parallelogramm ergibt sich:
Zwei Vektoren werden addiert, indem man ihre Repräsentanten "aneinanderhängt".
Aus dem dargestellten Parallelogramm ergibt sich: Zwei Vektoren werden subtrahiert, indem man
Zwei Vektoren werden subtrahiert, indem man Ein Vektor wird mit einem Skalar k multipliziert, indem man ihn um den Faktor k
streckt bzw. staucht.
Ein Vektor wird mit einem Skalar k multipliziert, indem man ihn um den Faktor k
streckt bzw. staucht.
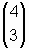
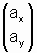
 Sind Anfangs- und Endpunkt des Vektors bekannt, so gilt:
Sind Anfangs- und Endpunkt des Vektors bekannt, so gilt: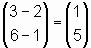
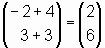 , der Endpunkt hat daher die Koordinaten D(2/6).
, der Endpunkt hat daher die Koordinaten D(2/6).
