 Das heißt:
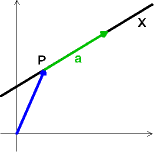
Das heißt:Ist von einer Geraden g ein Punkt P und ein Richtungsvektor a gegeben, so lautet die Gleichung der Geraden in Parameterform:
P und Q seien zwei Punkte in der Ebene. Setzt man in die Gleichung
X = P + t·PQ
für t verschiedene Zahlen ein, so erhält man für X immer einen Punkt auf der Geraden durch P und Q.
Umgekehrt kann man zu jedem Punkt auf der Geraden eine passende Zahl t finden. Wir haben also
eine Gleichung für die Gerade erhalten. t bezeichnet man als Parameter.
 Das heißt:
Das heißt:
Ist von einer Geraden g ein Punkt P und ein Richtungsvektor a gegeben,
so lautet die Gleichung der Geraden in Parameterform:
g: X = P + t·a
Beispiel: P(2/−1), a =
g: X =+ t·
Das können wir zeilenweise aufschreiben und parameterfrei machen:
x
y= 2 + 1·t
= −1 + 5·t| ·5
| ·(−1)5·x − y = 11 Das ist die Normalform der Geradengleichung.
Im Raum erhält man die Parameterform genauso. Es ist aber nicht möglich, eine Gerade durch eine einzige, parameterfreie Gleichung darzustellen.
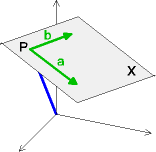 Eine Ebene ε im Raum ist durch einen Punkt P und zwei Richtungsvektoren a
und b bestimmt (die Vektoren dürfen nicht parallel sein). Die Gleichung der
Ebene enthält zwei Parameter u, v:
Eine Ebene ε im Raum ist durch einen Punkt P und zwei Richtungsvektoren a
und b bestimmt (die Vektoren dürfen nicht parallel sein). Die Gleichung der
Ebene enthält zwei Parameter u, v:
ε: X = P + u·a + v·b
Beispiel: Stelle die Gleichung der Ebene ε durch die Punkte P(1/1/3), Q(2/2/−2) und R(4/1/−3) auf!
PQ =, PR =
ε: X =+ u·
+ v·
Wenn man die Gleichung parameterfrei macht, erhält man die Normalform der Ebenengleichung:
x
y
z= 1 + u + 3·v
= 1 + u
= 3 − 5·u − 6·v| ·2 2·x + z
y= 5 − 3·u
= 1 + u
| ·32·x + 3·y + z = 8
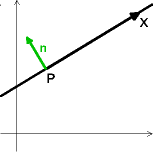 Ist von einer Geraden g ein Punkt P und ein Normalvektor n gegeben, so gilt für alle Punkte X
der Geraden:
Ist von einer Geraden g ein Punkt P und ein Normalvektor n gegeben, so gilt für alle Punkte X
der Geraden:
Die Vektoren n und PX stehen normal aufeinander, ihr Skalarprodukt ist also 0:
n·PX = 0
n·(X - P) = 0
n·X - n·P = 0
Die Gleichung der Geraden in Normalvektorform lautet daher:
g: n·X = n·P
Beispiel: P(2/-1), n =
g:·X =
·
Durch Ausmultiplizieren erhält man die Normalform der Geradengleichung:
4·x + 3·y = 5
Die Koordinaten des Normalvektors sind also die Koeffizienten von x und y in der Normalform!
Eine Gerade im Raum kann man nicht in der Normalvektorform darstellen, weil es im Raum keinen eindeutigen Normalvektor gibt.
Den Winkel zwischen zwei Geraden berechnet man nach der Formel:
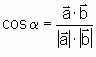
Dabei kann man die Richtungsvektoren oder die Normalvektoren der Geraden verwenden.
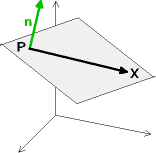 Ist von einer Ebene ein Punkt P und ein Normalvektor n bekannt,
so erhält man die Gleichung der Ebene in Normalvektorform ganz analog zur Geradengleichung:
Ist von einer Ebene ein Punkt P und ein Normalvektor n bekannt,
so erhält man die Gleichung der Ebene in Normalvektorform ganz analog zur Geradengleichung:
ε: n·X = n·P
Die Koordinaten des Normalvektors sind auch hier die Koeffizienten von x, y und z in der Normalform.
Beispiel: P(1/1/3), n =
ε:·X =
·
2·x + 3·y + z = 8
Lernziele
Übungen (Bsp. 15 - 22)