Juttas Matheseite - Kursunterlagen

Gleichungen mit einer Unbekannten

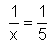Einen Ausdruck der Form

T₁(x) = T₂(x)

nennt man Gleichung mit der Unbekannten x. T₁ und T₂ sind dabei beliebige Terme. (Die Unbekannte kann natürlich auch anders benannt werden!)
Je nachdem, welche Zahl man für x einsetzt, erhält man eine wahre oder eine falsche Aussage.

Grundmenge: alle Zahlen, die zum Einsetzen in die Gleichung vorgesehen sind
Definitionsmenge: alle Elemente der Grundmenge, die für die Unbekannte eingesetzt werden dürfen
Lösungsmenge: alle Elemente der Definitionsmenge, die die Gleichung in eine wahre Aussage überführen

Beispiele:

3 · x + 1 = 10 G = ℕ D = ℕ L = {3}
x² = 4 G = ℕ D = ℕ L = {2}
x² = 4 G = ℝ D = ℝ L = {−2, 2}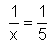
G = ℝ D = ℝ \ {0} L = {5}

Gleichungen, die dieselbe Lösungsmenge haben, heißen äquivalent.

Äquivalenzumformungen

Die Lösungsmenge einer Gleichung bleibt gleich, wenn man auf beiden Seiten

dieselbe Zahl (denselben Term) addiert bzw. subtrahiert,
mit derselben Zahl (demselben Term) ≠ 0 multipliziert,
durch dieselbe Zahl (denselben Term) ≠ 0 dividiert.

Wir werden immer versuchen, eine Gleichung durch Äquivalenzumformungen auf die einfachste Form zu bringen.
Dabei können Sonderfälle auftreten, z.B.:

x = x
Diese Aussage ist für alle Zahlen wahr ⇒ L = D

x = x + 1
Diese Aussage ist für alle Zahlen falsch ⇒ L = { }

Genauere Erklärungen: mathe online, Gleichungen
http://www.mathe-online.at/mathint/gleich/i.html
Abschnitte "Gleichung" - "Äquivalenzumformungen"

Lineare Gleichungen

Eine Gleichung der Form

a · x + b = 0

mit a, b ∈ R, a ≠ 0
heißt lineare Gleichung (d.h., x kommt nur in der ersten Potenz vor).
Sie hat in ℝ genau eine Lösung: L = {−b/a}

Beispiel:
(Wenn nicht anders angegeben, ist die Grundmenge immer ℝ)

7 · x − 6
= 4 · x + 9 | − 4 · x

3 · x − 6
= 9 | + 6

3 · x
= 15 | :3

x
= 5

L = {5}

Lernziele

Ich weiß, was eine Gleichung ist.
Ich weiß, was die Lösung einer Gleichung ist.
Ich kann eine lineare Gleichung durch Äquivalenzumformungen lösen.

Genauere Erklärungen: mathe online, Gleichungen
http://www.mathe-online.at/mathint/gleich/i.html
Abschnitte "Lineare Gleichungen", "Normalform der linearen Gleichung"

Übungen
Textbeispiele

Weiter: Quadratische Gleichungen

3 · x + 1 = 10	G = ℕ	D = ℕ	L = {3}
x² = 4	G = ℕ	D = ℕ	L = {2}
x² = 4	G = ℝ	D = ℝ	L = {−2, 2}
	G = ℝ	D = ℝ \ {0}	L = {5}

7 · x − 6	= 4 · x + 9	\| − 4 · x
3 · x − 6	= 9	\| + 6
3 · x	= 15	\| :3
x	= 5
L = {5}