Potenzen und Wurzeln

Rechenregeln für Potenzen

Rechenstufen bei Potenzen und Hochzahlen Definition: an = a · a · ... · a (n Faktoren)
a ... Basis
n ... Hochzahl (Exponent)


Rechenregeln für Potenzen mit gleicher Basis:

am · an = am + n
am : an = am - n
(am)n = am·n

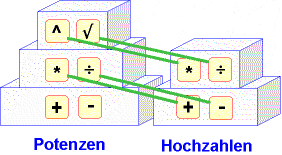
Einer Rechenart 2. (3.) Stufe entspricht also, wenn man nur die Hochzahlen betrachtet, eine Rechenart 1. (2.) Stufe.

Weitere Rechenregeln:

(a · b)n = an · bn
(a/b)^n = a^n/b^n

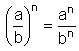
Nach der obigen Definition kann der Exponent nur eine natürliche Zahl sein. Ziel dieses Kapitels ist die Antwort auf die Frage: Haben auch Ausdrücke wie a-3 oder a1/2 einen Sinn? Prinzipiell könnten wir diese Ausdrücke beliebig definieren - allerdings sollen diese Definitionen auch sinnvoll sein, das heißt, die bekannten Rechenregeln sollen weiter gelten.

Potenzen mit ganzzahligen Exponenten

Was bedeutet a0? Dieser Ausdruck könnte z.B. als Ergebnis der folgenden Rechnung auftreten:

a1 : a1 = a1 - 1 = a0

Andrerseits ist a1 : a1 = 1, also erhalten wir: a0 = 1 (jede Zahl hoch 0 ist 1).

Ebenso ist

a1 : a2 = a1 - 2 = a-1,

andrerseits ist a1 : a2 = 1/a, also ist a-1 = 1/a.

Daher definiert man

a0 = 1
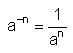
a^-n = 1/a^n

Eine negative Hochzahl bedeutet also, dass die Potenz (mit positiver Hochzahl) in den Nenner geschrieben wird (bzw. der Kehrwert gebildet wird).

Rechnen mit Wurzeln

Definition: Die n-te Wurzel einer Zahl a (n√a) ist die nicht negative Lösung der Gleichung xn = a.
(Wegen der Eindeutigkeit beschränken wir uns auf nicht negative Zahlen a und x.)

Rechenregeln:

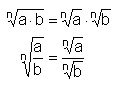
n.Wurzel(a*b) = n.Wurzel(a)*n.Wurzel(b) n.Wurzel(a/b) = n.Wurzel(a)/n.Wurzel(b)

Einige Tricks zum Rechnen mit Wurzeln:

Teilweises Wurzelziehen:
Auch wenn eine Wurzel nicht ganzzahlig ist, können wir sie oft so umformen, dass unter der Wurzel eine möglichst kleine Zahl übrigbleibt.
Beispiel: √12 = √(4·3) = √4·√3 = 2√3

Rationalmachen des Nenners:
Mit einem Bruch, bei dem im Nenner eine Wurzel steht, kann man schlecht rechnen. Daher erweitern wir so, dass der Nenner rational wird:
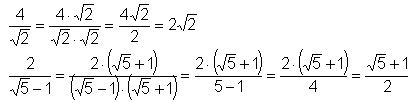
4/Wurzel(2) = (4*Wurzel(2))/(Wurzel(2)*Wurzel(2)) = 4*Wurzel(2))/2 = 2*Wurzel(2)

Potenzen mit rationalen Exponenten

Was bedeutet a1/2? Wir können rechnen:

a1/2 · a1/2 = a1/2 + 1/2 = a1 = a

Die Zahl, die mit sich selbst multipliziert a ergibt, ist aber √a. Das heißt: a1/2 = √a.

Analog definiert man

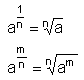
a^(1/n) = n.Wurzel(a) a^(m/n) = n.Wurzel(a^n)

Die Rechenregeln für Wurzeln sind also Sonderfälle der Rechenregeln für Potenzen.

Lernziele

Ausführliche Erklärung: mathe online, Potenzen http://www.mathe-online.at/mathint/pot/i.html

Online-Kurs über Potenzen (mit interaktiven Tests): http://www.johnny.ch/ot/index.htm
(Bei den Tests kannst du einen beliebigen Usernamen angeben.)

Übungen