Potenzfunktionen
f(x) = xn
(siehe auch "Potenzen und Wurzeln")
Natürliche Exponenten: |
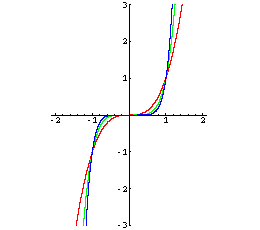
Ungerade Hochzahlen:
Der Graph beschreibt eine S-Kurve und ist symmetrisch zum Koordinatenursprung. |
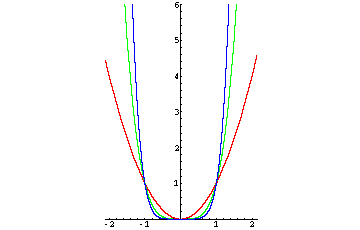
Gerade Hochzahlen:
Der Graph ähnelt einer Parabel und ist symmetrisch zur y-Achse. |
|
|
f3: x → x3
f5: x → x5
f7: x → x7 |
f2: x → x2
f4: x → x4
f6: x → x6 |
Negative Exponenten: |
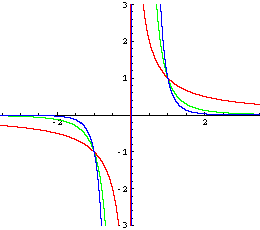
Ungerade Hochzahlen:
Der Graph ähnelt einer Hyperbel und ist symmetrisch zum Koordinatenursprung
(für x = 0 nicht definiert!) |
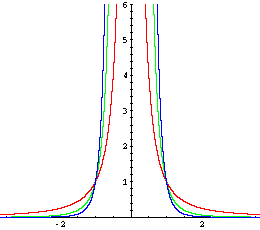
Gerade Hochzahlen:
Der Graph ist symmetrisch zur y-Achse
(für x = 0 nicht definiert!) |
|
|
f-1: x → x-1 = 1/x
f-3: x → x-3 = 1/x3
f-5: x → x-5 = 1/x5 |
f-2: x → x-2 = 1/x2
f-4: x → x-4 = 1/x4
f-6: x → x-6 = 1/x6 |
Rationale Exponenten (0 < n < 1): |
|
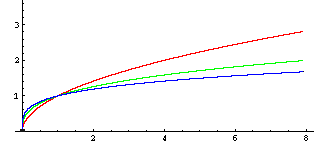
Hier handelt es sich um Wurzelfunktionen. Sie sind nur für x ≥ 0 definiert.
Der Graph entsteht, indem man den Graphen der entsprechenden Potenzfunktion an der 1. Mediane spiegelt. |
|
f1/2: x → x1/2 = √x
f1/3: x → x1/3 = 3√x
f1/4: x → x1/4 = 4√x
|
Zusammenhänge zwischen Größen
Bei einer Funktion der Form y = a·x sagt man:
x und y sind direkt proportional zueinander
(je größer x, umso größer y; wenn x verdoppelt, verdreifacht ... wird, wird y auch verdoppelt, verdreifacht ...).
Bei einer Funktion der Form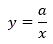 
sagt man:
x und y sind indirekt proportional zueinander
(je größer x, umso kleiner y; wenn x verdoppelt, verdreifacht ... wird, wird y halbiert, gedrittelt ...).
Auch andere Arten von Zusammenhängen sind möglich, z.B. y ist direkt proportional zu x2.
Siehe auch: mathe online, Graphen einfacher Potenzfunktionen
http://www.mathe-online.at/galerie/fun1/fun1.html#graphenpf
Lernziele:
- Ich erkenne die Graphen von Potenz- und Wurzelfunktionen.
- Ich kann die Graphen von Potenz- und Wurzelfunktionen skizzieren.
- Ich finde zu einer Anwendungssituation den passenden Funktionstyp.
Übungen: Weihnachtsbäckerei (Zusammenhänge zwischen Größen)
Weiter: Exponential- und Logarithmusfunktionen