f(x) = a·x2 + b·x + c (a, b, c ∈ ℝ)
heißt quadratische Funktion.
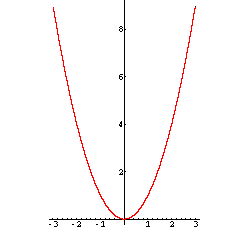
f(x) = x2
Der Graph ist eine Parabel mit dem Scheitel im Koordinatenursprung (die sog. Normparabel).
Schieberegeln:
Der Graph der Funktion f(x) + d / f(x) − d entsteht, indem der Graph der Funktion f(x) um d Einheiten nach oben / unten verschoben wird.
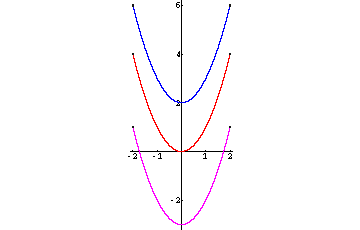
Beispiel:
f1: x → x2
f2: x → x2 + 2
f3: x → x2 − 3
Der Graph der Funktion f(x − e) / f(x + e) entsteht, indem der Graph der Funktion f(x) um e Einheiten nach rechts / links (!) verschoben wird.
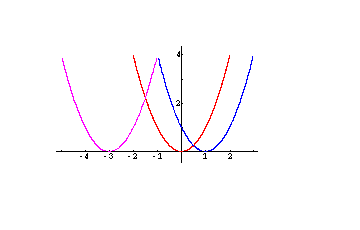
Beispiel:
f1: x → x2
f2: x → (x − 1)2
f3: x → (x + 3)2
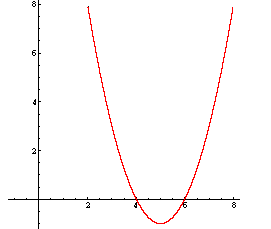Durch geeignete Umformungen kann man jede quadratische Funktion auf eine solche Form bringen, z.B.:
f(x) = x2 − 10x + 24
(Ergänzen auf ein vollständiges Quadrat)
= x2 − 10x + 25 − 25 + 24
= (x − 5)2 − 1
Die Normparabel wurde also um 5 Einheiten nach rechts und um 1 Einheit nach unten verschoben. Der Graph ist daher eine Parabel mit dem Scheitel S(5/−1).
Multipliziert man die Funktion mit einer Konstanten, so wird der Graph in y-Richtung gestreckt bzw. gestaucht; bei Multiplikation mit −1 wird der Graph an der x-Achse gespiegelt. Wir stellen daher zusammenfassend fest:
Der Graph der quadratischen Funktion
f(x) = a·x2 + b·x + c
ist eine Parabel, und zwar
für a > 0 nach oben offen,
für a < 0 nach unten offen.
Wenn die Koordinaten des Scheitels S = (xS/yS) bekannt sind, kann man die Funktionsgleichung in der Scheitelform schreiben:
Scheitelform der quadratischen Funktion
f(x) = a·(x − xS)2 + yS
Lernziele