Funktionen

Grundbegriffe

Eine Funktion ist eine Vorschrift, durch die jedem Element der Definitionsmenge genau ein Element der Wertemenge zugeordnet wird.

Das Element der Definitionsmenge - das Argument bzw. die unabhängige Variable - bezeichnet man meist mit x, das zugeordnete Element der Wertemenge - den Funktionswert bzw. die abhängige Variable - mit y.
Die Zuordnungsvorschrift besteht oft aus einem Term.

Beispiel:
1 kg Äpfel kostet 2 €. Wieviel kosten x kg?

Bezeichnen wir die Menge mit x, den Preis mit y, so lautet die Zuordnungsvorschrift:

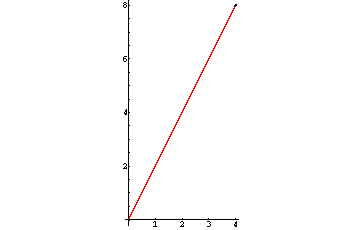
y = 2·x

Zu jeder Menge gehört genau ein Preis. Es handelt sich daher um eine Funktion (wir nennen sie f).
Die Definitionsmenge und die Wertemenge sind R⁺₀ (positive reelle Zahlen mit 0), da Menge bzw. Preis nicht negativ sein können.

Wertetabelle:

x	y
0	0
1	2
2	4
3	6
4	8

Fassen wir die Zahlenpaare (x/y) als Koordinaten auf, so bilden die entsprechenden Punkte den Graphen der Funktion. In diesem Beispiel ist der Graph eine Gerade.

Wir können eine Funktion also angeben durch

• eine Wertetabelle
• einen Funktionsterm
• den Graphen.

Schreibweisen:

• f: y = 2·x
• f: x → 2·x       ("x wird abgebildet auf 2·x")
• f(x) = 2·x       ("Der Funktionswert von x ist 2·x" oder kurz "f von x ist 2·x")

Weitere Beispiele für Funktionen

1. Der freie Fall eines Körpers lässt sich (angenähert) durch die Formel

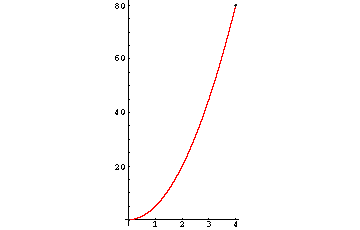
   s = 5·t²

   beschreiben (t: Zeit in sec, s: Weg in m). Der Weg ist also eine Funktion der Zeit.

   Wertetabelle:

   t	s
   0	0
   1	5
   2	20
   3	45
   4	80

   
   

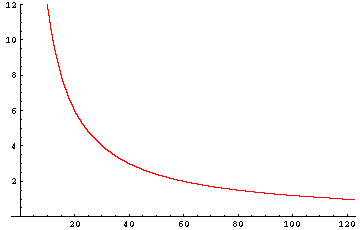
2. Eine Strecke von 120 km soll zurückgelegt werden. Die Fahrzeit hängt dabei von der Geschwindigkeit ab:

   t = 120/v

   (v: Geschwindigkeit in km/h, t: Zeit in h).

   Wertetabelle:

   v	t
   10	12
   20	6
   30	4
   40	3
   60	2
   80	1,5
   100	1,2
   120	1

Einige wichtige Begriffe:

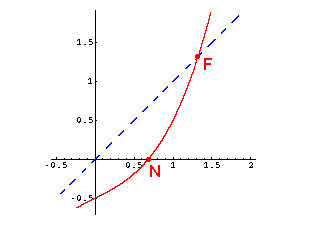Nullstelle: Stelle, an der f(x) = 0
graphisch: Schnittpunkt des Graphen mit der x-Achse

Fixwert: Stelle, an der f(x) = x
graphisch: Schnittpunkt des Graphen mit der 1. Mediane (das ist die Gerade, die den Winkel zwischen der positiven x-Achse und der positiven y-Achse halbiert)

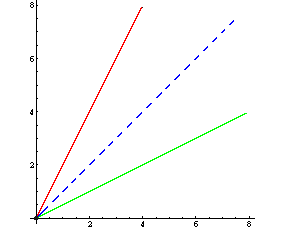Umkehrfunktion:
Im ersten Beispiel entspricht auch jedem Preis genau eine Menge (z.B.: für 5 € erhält man 2,5 kg Äpfel). Die Menge ist also auch eine Funktion des Preises:

x = y/2

Wenn man - der Einheitlichkeit halber - die unabhängige Variable wieder mit x bezeichnet, lautet die Gleichung der Umkehrfunktion

f⁻¹: y = x/2

Den Graphen der Umkehrfunktion erhält man, indem man den Graphen von f an der 1. Mediane spiegelt.
Allgemein gilt:
Eine Funktion ist umkehrbar, wenn jedem y-Wert genau ein x-Wert entspricht; die Gleichung der Umkehrfunktion erhält man, indem man x und y vertauscht.

Implizite Funktion:
Durch die Gleichung

x + y = 5

wird eine Funktion festgelegt (zu jedem Wert für x gibt es genau einen Wert für y).

Das bezeichnet man als implizite Darstellung einer Funktion. Die explizite Darstellung erhält man, indem man die Gleichung nach y auflöst:

y = 5 − x

Übungen

Ausführliche Erklärung: mathe online, Funktionen http://www.mathe-online.at/mathint/fun1/i.html