![]()
Außer der Untersuchung von Kurven (Wurfbahnen, durchhängende Seile, belastete Träger, Kostenfunktionen ...) gibt es noch einige weitere Anwendungen, die für die Schulmathematik wichtig sind.
Wenn eine Wegfunktion s(t) gegeben ist (das heißt, der Abstand s eines Körpers von einem beliebig gewählten Nullpunkt abhängig vom Zeitpunkt t), können wir die mittlere Geschwindigkeit (Durchschnittsgeschwindigkeit) im Zeitintervall [t1, t2] berechnen:
Das ist der Differenzenquotient der Wegfunktion. Wenn wir die Zeitdifferenz Δt gegen Null gehen lassen, erhalten wir als Differentialquotient die Momentangeschwindigkeit v(t) zu einem bestimmten Zeitpunkt.
Analog definiert man die mittlere Beschleunigung als Änderung der Geschwindigkeit:
und als Grenzwert davon die Momentanbeschleunigung a(t). Zusammengefasst:
| Weg: | s(t) |
| Geschwindigkeit: | v(t) = s'(t) |
| Beschleunigung: | a(t) = v'(t) = s''(t) |
Beispiele:
Bei einem Experiment wird eine Kugel von der Marsoberfläche nach oben geschossen. Ihre Höhe abhängig von der Zeit wird durch die folgende Funktion dargestellt:
s(t) = 18,5·t − 1,85·t2
(t: Zeit in Sekunden, s(t): Höhe in Meter)
Wann trifft die Kugel wieder auf dem Boden auf?
s(t) = 0
t1 = 0, t2 = 10 ⇒ nach 10 Sekunden
Mit welcher Geschwindigkeit wurde die Kugel abgeschossen?
v(t) = s'(t) = 18,5 − 3,7·t
v(0) = 18,5 − 3,7·0 = 18,5 ⇒ mit 18,5 m/s
Berechne die mittlere Geschwindigkeit in den ersten 3 Sekunden.
s(0) = 18,5·0 − 1,85·02 = 0
s(3) = 18,5·3 − 1,85·32 = 38,85
Die Kugel hat in 3 Sekunden 38,85 Meter zurückgelegt, im Durchschnitt also 38,85/3 = 12,95 m/s.
Welche maximale Höhe erreicht die Kugel?
Um das Maximum (den Hochpunkt) zu finden, müssen wir die 1. Ableitung gleich Null setzen:
s'(t) = 0 ⇒ t = 5 s
Die maximale Höhe wird nach 5 Sekunden erreicht. Das Ergebnis setzen wir in s(t) ein:
s(5) = 18,5·5 − 1,85·52 = 46,25 m
Wie hoch ist die Fallbeschleunigung auf dem Mars?
a(t) = s''(t) = − 3,7
Das negative Vorzeichen ergibt sich daraus, dass die Höhe nach oben gemessen wird, die Schwerkraft aber nach unten wirkt.
Die Beschleunigung beträgt 3,7 m/s2.
Ein Auto fährt mit 72 km/h auf der Bundesstraße. Es beschleunigt kurz, um einen LKW zu überholen.
Nach 10 Sekunden hat es mit 90 km/h die maximale Geschwindigkeit erreicht und bremst danach wieder ab.
Der zurückgelegte Weg kann in diesem Zeitraum durch eine Polynomfunktion 3. Grades angenähert werden.
Erstelle ein Gleichungssystem zur Ermittlung der Koeffizienten dieser Funktion und ermittle die Funktionsgleichung.
Zuerst rechnen wir alle Geschwindigkeiten in Meter pro Sekunde um (1 m/s = 3,6 km/h):
72 km/h = 72/3,6 m/s = 20 m/s, 90 km/h = 90/3,6 m/s = 25 m/s
s(t) = a·t3 + b·t2 + c·t + d
s'(t) = 3a·t2 + 2b·t + c
s''(t) = 6a·t + 2b
(s: Zeit in Sekunden, s: Weg in Meter, jeweils ab Beginn des Überholvorgangs)
Zu Beginn wurde noch kein Weg zurückgelegt:
s(0) = 0 ⇒ a·03 + b·02 + c·0 + d = 0
Zu Beginn beträgt die Geschwindigkeit 20 m/s:
s'(0) = 20 ⇒ 3a·02 + 2b·0 + c = 20
Nach 10 Sekunden beträgt die Geschwindigkeit 25 m/s:
s'(10) = 25 ⇒ 3a·102 + 2b·10 + c = 25
Nach 10 Sekunden ist die Geschwindigkeit maximal, das heißt, die Wegfunktion hat an dieser Stelle einen Wendepunkt:
s''(10) = 0 ⇒ 6a·10 + 2b = 0
Das ergibt folgendes Gleichungssystem:
d = 0
c = 20
300a + 20b + c = 25
60a + 2b = 0
Wenn wir es lösen, erhalten wir die Funktion
In der Praxis wird man oft vor die Aufgabe gestellt, eine Größe (Fläche, Volumen, Materialverbrauch, Kosten... ) zu optimieren. Wenn wir die Größe durch eine Funktion in einer Variablen ausdrücken können, können wir mit Hilfe der Ableitung den Extremwert berechnen. Wenn mehrere Variablen vorkommen, müssen wir diese zuerst durch eine ausdrücken.
Schema zum Lösen einer Extremwertaufgabe:
Beispiele:
Entlang einer Mauer soll eine rechteckige Fläche von 50 m2 eingezäunt werden. Wie lang müssen die Seiten des Rechtecks sein, damit man möglichst wenig Zaun braucht?
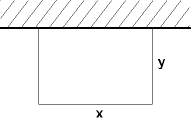
| Zielfunktion: | u(x,y) = x + 2·y → Minimum |
| Nebenbedingung: | x·y = 50 y = 50·x−1 |
| einsetzen: | u(x) = x + 100·x−1 |
| differenzieren: | u'(x) = 1 − 100·x−2 u''(x) = 200·x−3 |
| Minimum berechnen: | 1 − 100·x−2 = 0 x = 10, y = 5 |
| Kontrolle: | u''(10) = 200/1000 > 0 ⇒ Minimum |
Welches von allen Rechtecken, die man einem Kreis vom Radius r einschreiben kann, hat den größten Flächeninhalt?
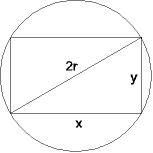
| Zielfunktion: | A(x,y) = x·y → Maximum |
| Nebenbedingung: | x2 + y2 = 4·r2 y = √(4r2 − x2) |
| einsetzen: | A(x) = x·√(4·r2 − x2) |
| vereinfachen: | A~(x) = x2·(4·r2 − x2) = 4·r2·x2 − x4 |
| differenzieren: | A~'(x) = 8·r2x − 4·x3 A~''(x) = 8·r2 − 12·x2 |
| Maximum berechnen: | 8·r2·x − 4·x3 = 0 x = r√2, y = r√2 (Quadrat) (x = 0 und die negative Lösung kommen nicht in Frage) |
| Kontrolle: | A~''(r√2) = −16·r2 < 0 ⇒ Maximum |
Einem Kegel vom Radius R und der Höhe H werden Zylinder eingeschrieben. Welcher von diesen Zylindern hat das größte Volumen?
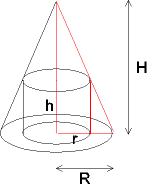
| Zielfunktion: | V(r,h) = r2·π·h → Maximum |
| Nebenbedingung: | Die roten Dreiecke sind ähnlich:
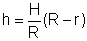 |
| einsetzen: | 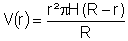 |
| vereinfachen: | V~(r) = r2·(R−r) = R·r2 − r3 |
| differenzieren: | V~'(r) = 2·R·r − 3·r2 V~''(r) = 2·R − 6·r |
| Maximum berechnen: | 2·R·r − 3·r2 = 0 r1 = 0, r2 = 2·R/3 |
| Kontrolle: | V~''(0) = 2·R > 0 ⇒ Minimum V~''(2R/3) = −2·R < 0 ⇒ Maximum r = 2·R/3, h = H/3 |
Links:
http://www.mathe-online.at/mathint/anwdiff/i.html#Extremwertaufgaben:
ausführliche Erklärung
http://www.mathe-online.at/mathint/anwdiff/i_ExtrAufg.html: ein Beispiel
http://www.mathe-online.at/materialien/matroid/files/ex/ex.html: ausführliche Erklärung mit vielen
Beispielen
Übungen:
Verschiedene Anwendungen - Extremwertaufgaben