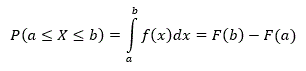Stetige Wahrscheinlichkeitsverteilungen

Eine stetige Zufallsvariable kann (in einem bestimmten Bereich) jeden beliebigen Wert annehmen. Man kann sie durch ihre Dichtefunktion f oder durch die Verteilungsfunktion F beschreiben (die Dichtefunktion ist die Ableitung der Verteilungsfunktion). Die Wahrscheinlichkeit, dass X zwischen a und b liegt, entspricht der Fläche unter der Kurve, also dem Integral:

.

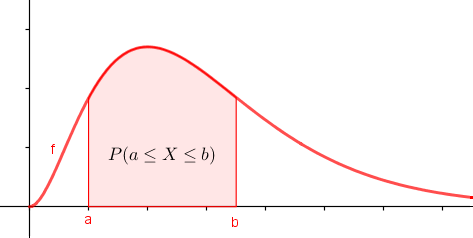
Die gesamte Fläche unter der Kurve ist 1 (sicheres Ereignis). Die Wahrscheinlichkeit, dass X einen bestimmten Wert annimmt, ist bei stetigen Verteilungen 0. Daher ist es egal, ob man P(X < a) oder P(X ≤ a) berechnet.

Auch Erwartungswert und Standardabweichung einer stetigen Verteilung werden mit Hilfe des Integrals definiert.

Die Normalverteilung

Die wichtigste stetige Wahrscheinlichkeitsverteilung ist die von C. F. Gauß (1777 - 1855) entdeckte Normalverteilung mit der Dichtefunktion:

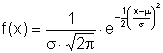
μ: Erwartungswert, σ: Standardabweichung

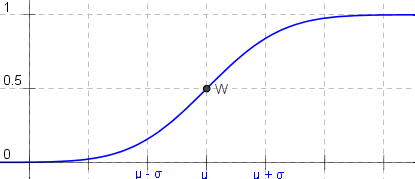
Sie tritt bei vielen Größen im Alltag auf. Der Graph der Dichtefunktion (links) ist die bekannte "Glockenkurve" ; sie besitzt einen Hochpunkt bei μ und zwei Wendepunkte bei μ ± σ. Der Erwartungswert gibt also an, wo der Gipfel der Verteilung liegt; die Standardabweichung bestimmt die Form der Kurve (hoch und schmal oder niedrig und breit.)
Die Verteilungsfunktion (rechts) ist eine s-förmige Kurve mit einem Wendepunkt W = (μ / 0,5).

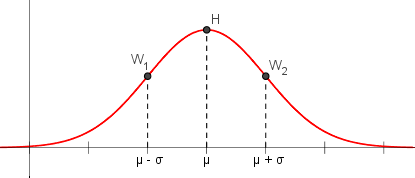
Es gilt folgende Faustregel:

P(μ − σ ≤ X ≤ μ + σ) = 68 % ≈ ²/₃
P(μ − 2·σ ≤ X ≤ μ + 2·σ) = 95 %
P(μ − 3·σ ≤ X ≤ μ + 3·σ) > 99 %

Die Wahrscheinlichkeiten für beliebige Werte kann man mit dem Taschenrechner oder anderer Technologie berechnen. Der entsprechende Befehl lautet "normalCdf" oder ähnlich. Wenn die Wahrscheinlichkeit gegeben ist und der dazugehörige x-Wert gesucht wird, braucht man die Umkehrfunktion "invNorm".

Berechnung der Normalverteilung mit Tabelle

Wenn man keine Technologie zur Verfügung hat, muss man eine Tabelle der Standardnormalverteilung φ mit Erwartungswert 0 und Standardabweichung 1 verwenden (z.B. hier).

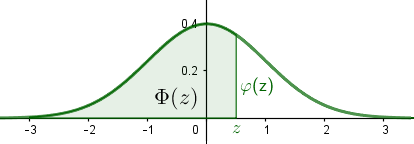
In der Tabelle sind die Werte der Verteilungsfunktion Φ angeführt, also die Wahrscheinlichkeit, dass die normierte Zufallsvariable Z ≤ z ist:
P(Z ≤ z) = Φ(z)

Eine beliebige Normalverteilung kann man durch die Standardisierungsformel

in die Standardnormalverteilung umrechnen.

Beispiel: Eine Machine erzeugt Nägel mit einer durchschnittlichen Länge von μ = 50 mm. Die Länge der Nägel ist normalverteilt, die Standardabweichung beträgt σ = 2,5 mm.

• Wieviel Prozent aller Nägel sind kürzer als 48 mm?
  Normierung: z = (48 − 50)/2,5 = −0,8
  Wegen der Symmetrie der Glockenkurve ist Φ(−z) = 1 − Φ(z).
  P(X < 48) = Φ(−0,8) = 1 − Φ(0,8) = 0,2119 = 21,19%

• Wieviel Prozent aller Nägel sind länger als 51 mm?
  z = (51 − 50)/2,5 = 0,4
  "länger als 51 mm" ist das Gegenereignis zu "höchstens 51":
  P(X > 51) = 1 − Φ(0,4) = 0,3446 = 34,46%

• Wieviel Prozent aller Nägel sind zwischen 48 und 51 mm lang?
  P(48 ≤ X ≤ 51) = Φ(0,4) − Φ(−0,8) = 0,4435 = 44,35%

• Wie lang muss ein Nagel sein, damit er zu den 10% kürzesten gehört?
  Φ(z) = 0,1 ⇒ z = Φ⁻¹(0,1) = −Φ⁻¹(0,9) = −1,28
  x = 50 − 1,28·2,5 = 46,8 ⇒ er darf höchstens 46,8 mm lang sein.

• In welchem symmetrischen Bereich (μ − ε, μ + ε) liegt die Länge von 90% aller Nägel?
  Wenn 90 % in diesem Bereich liegen, müssen jeweils 5 % darunter und darüber liegen. Für die obere Grenze gilt daher:
  Φ(z) = 0,95 ⇒ z = Φ⁻¹(0,95) = 1,64
  untere Grenze: x₁ = 50 − 1,64·2,5 = 45,9
  obere Grenze: x₂ = 50 + 1,64·2,5 = 54,1
  90% aller Nägel sind zwischen 45,9 mm und 54,1 mm lang.

Annäherung der Binomialverteilung durch die Normalverteilung

Wenn die Anzahl der Versuche sehr groß ist, wird die Berechnung der Binomialverteilung zu aufwändig. Man kann sie dann näherungsweise durch die Normalverteilung mit demselben μ und σ ersetzen.
(Faustregel: σ muss ≥ 3 sein.)

Beispiel:

Wie groß ist die Wahrscheinlichkeit, bei 300-maligem Würfeln höchstens 40 mal Sechs zu werfen?
n = 300, p = ¹/₆ ⇒ μ = 300·¹/₆ = 50, σ = √(300·¹/₆·⁵/₆) = 6,45
z = (40 − 50)/6,45 = −1,55
P(X ≤ 40) = Φ(−1,55) = 0,0606

Die Annnäherung wird noch genauer, wenn man die Stetigkeitskorrektur berücksichtigt.
Im Histogramm der Binomialverteilung reicht z.B. der Streifen, der X = 40 entspricht, von 39,5 bis 40,5.
Für die Berechnung von P(X ≤ 40) nimmt man daher 40,5 als obere Grenze.
Für P(40 ≤ X ≤ 50) nimmt man die Grenzen 39,5 und 50,5.

Im obigen Beispiel erhält man mit Stetigkeitskorrektur:
z = (40,5 − 50)/6,45 = −1,47
P(X ≤ 40) = Φ(−1,47) = 0,0708

Die genaue Berechnung mit Binomialverteilung ergibt 0,0675.)

Weitere stetige Wahrscheinlichkeitsverteilungen

Übungen