Rechnen mit Termen

Grundbegriffe

Eine Variable (a, b, x ...) ist ein Platzhalter für eine Zahl.
Ein Term ist ein sinnvoller mathematischer Ausdruck aus Zahlen, Variablen und Rechenzeichen.

Beispiele: 7, 2·x + 3, a³ − 3·b² + 1, , ...

(Der Malpunkt wird meist weggelassen: 2·x = 2x, a·b = ab.)

Definitionsmenge eines Terms: alle Zahlen, die für die Variable(n) eingesetzt werden dürfen. Dabei muss man darauf achten, dass z.B. der Nenner eines Bruchterms nicht 0 sein darf.

Ein Term, der Variablen enthält, nimmt einen bestimmten Wert an, wenn man für die Variablen Zahlen einsetzt (man nennt das: Belegen der Variablen).

Beispiel:
T(x) = 2x + 3 (sprich: T von x)       D = {1, 2, 3, 4, 5}

x	T(x)
1	2·1 + 3 = 5
2	2·2 + 3 = 7
3	2·3 + 3 = 9
4	2·4 + 3 = 11
5	2·5 + 3 = 13

Zwei Terme sind äquivalent, wenn sie bei jeder Belegung denselben Wert annehmen.

Beispiel: 2x + 3x = 5x
Wir werden immer versuchen, einen Term in einen möglichst einfachen äquivalenten Term umzuformen.

Wichtige Begriffe:
Monom: eingliedriger Term, z.B. 2ab
Polynom: mehrgliedriger Term, z.B. x³ + 2x² - 4x − 1
Koeffizienten: Zahlen, mit denen die Variablen multipliziert werden (hier: 1, 2, −4)
Grad des Polynoms: höchste vorkommende Potenz
Zweigliedrige Terme nennt man auch Binom.
Außerdem gibt es noch Bruchterme, Wurzelterme u.v.m.

Addition und Subtraktion von Termen

Man kann nur gleichartige Termglieder addieren bzw. subtrahieren (Basis und Hochzahl gleich)!

Beispiel:

2a + 4b + 3a − 2b =
= 2a + 3a + 4b − 2b =	(KG)
= (2 + 3)·a + (4 − 2)·b =	(DG)
= 5a + 2b
x2 - 3x + 4 + 5x + 2x2 =
= x2 + 2x2 − 3x + 5x + 4 =	(KG)
= (1 + 2)·x2 + (−3 + 5)·x + 4 =	(DG)
= 3x2 + 2x + 4

Falsch wäre z.B.:
2a + 3b = 5?
3x² + 4x = 7x^?

Auflösen von Klammern:
Steht vor der Klammer ein +, kann man die Klammer weglassen.
Steht vor der Klammer ein − , muss man beim Weglassen der Klammer alle Vorzeichen ändern.

Beispiel: 3a + (2b - c) - (2a + 3c - b) = 3a + 2b - c - 2a - 3c + b = a + 3b - 4c

Multiplikation von Termen

Potenzen mit gleicher Basis werden multipliziert, indem man die Hochzahlen addiert.

Beispiel:
4x²·5x³ = 4·5·(x·x)·(x·x·x) = 20x⁵

Das Produkt eines Monoms mit einem Polynom berechnet man nach dem Distributivgesetz.

a·(c + d) = a·c + a·d
bzw.
a·(e − d) = a·e − a·d

Beispiele:
2·(2x - 3y) = 4x − 6y
ab·(a² - ab + b²) = a³b - a²b² + ab³

Produkt zweier Polynome:
Jedes Glied des ersten Terms wird mit jedem Glied des zweiten Terms multipliziert.

(a + b)·(c + d) = ac + bc + ad + bd

Beispiele:
(3a + 4)·(2a − 1) = 3a·2a + 4·2a + 3a·(−1) + 4·(−1) = 6a² + 8a − 3a - 4 = 6a² + 5a − 4
(x² + 2x − 3)·(x + 5) = x²·x + 2x·x − 3·x + x²·5 + 2x·5 − 3·5 = x³ + 2x² − 3x + 5x² + 10x − 15 = x³ + 7x² + 7x - 15

Potenzieren von Binomen

Durch Ausmultiplizieren erhält man die binomischen Formeln (wichtig!):

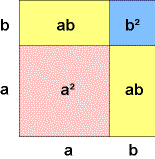
(a + b)2 = a2 + 2ab + b2 (a − b)2 = a2 − 2ab + b2 (a + b)·(a − b) = a2 - b2

 

Beispiel: (2x + 3)² = (2x)² + 2·2x·3 + 3² = 4x² + 12x + 9

Für höhere Potenzen findet man die Koeffizienten mithilfe des Pascal'schen Dreiecks.

Übungen

Terme zerlegen

• Herausheben gemeinsamer Faktoren:

  Umkehrung des Distributivgesetzes
  z.B.: 2a + 4b − 6c = 2·(a + 2b − 3c)
  Der Faktor 2 ist in allen Summanden enthalten, also kann man ihn vor die Klammer schreiben; beim Ausmultiplizieren muss man wieder den ursprünglichen Term erhalten

• Zerlegen mithilfe der binomischen Formeln:

  z.B.: 9x² + 6x + 1 = (3x + 1)²
  25a² − 16b² = (5a + 4b)·(5a − 4b)

• Terme dividieren:

  Vergleiche dazu Division von Zahlen:
  Wir schreiben jetzt alle Zwischenschritte an, auch die, die wir normalerweise im Kopf durchführen:

  276	: 12 = 23	12 in 27 = 2mal
  − 24		2·12 = 24 (abziehen)
  36		12 in 36 = 3mal
  − 36		3·12 = 36 (abziehen)
  0

  Analog rechnet man mit Polynomen:

  (x2 + 5x + 6)	: (x + 2) = x + 3	x2 : x = x
  −x2 +−2x		x·(x + 2) = x2 + 2x (abziehen)
  3x + 6		3x : x = 3
  −3x +−6		3·(x + 2) = 3x + 6 (abziehen)
  0

  Probe durch Ausmultiplizieren!

  Anmerkung: Das Horner-Schema ist eine einfachere Methode, durch ein Polynom zu dividieren.

Übungen