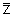Komplexe Zahlen

Definition

Bekanntlich haben quadratische Gleichungen nicht immer eine reelle Lösung. Wenn man will, dass quadratische Gleichungen (und solche höheren Grades) ohne Einschränkungen lösbar sein sollen, muss man eine neue Art von Zahlen einführen.

Wir definieren die imaginäre Einheit i durch die Gleichung

i² = −1

(Das ist keine reelle Zahl, weil das Quadrat einer rellen Zahl immer positiv oder 0 ist.)
Vielfache von i heißen imaginäre Zahlen (z.B. 2·i, −0,5·i, √3·i).
Eine Zahl der Form z = a + b·i (a, b in ℝ) heißt komplexe Zahl (z.B. 4 + 3·i, 1,8 − 0,5·i). Dabei ist a der Realteil und b der Imaginärteil von z. Man schreibt auch kürzer z = (a, b).
Die Menge aller komplexen Zahlen bezeichnet man mit ℂ. Die Menge ℝ ist eine Teilmenge von ℂ; sie besteht aus allen Zahlen, deren Imaginärteil 0 ist.

Beispiel: Die Gleichung x² − 2·x + 10 = 0 hat die Lösungen
x_1,2 = 1 ± √−9 = 1 ± 3·√−1, also
x₁ = 1 + 3·i, x₂ = 1 − 3·i

Zwei solche Zahlen, die sich nur durch das Vorzeichen des Imaginärteils unterscheiden, heißen konjugiert komplex, mit anderen Worten: die zu 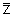z = a + b·i konjugiert komplexe Zahl ist = a − b·i (sprich "z quer").

Rechnen mit komplexen Zahlen

Bei Addition, Subtraktion und Multiplikation gelten dieselben Rechenregeln wie beim Rechnen mit Termen. Wenn in der Rechnung i² auftritt, wird es durch −1 ersetzt.

Beispiel:
(2 + i) + (1 + 3·i) = 2 + i + 1 + 3·i = 3 + 4·i
(2 + i) − (1 + 3·i) = 2 + i − 1 − 3·i = 1 − 2·i
(2 + i)·(1 + 3·i) = 2 + i + 6·i + 3·i² = −1 + 7·i

Wenn man durch eine komplexe Zahl dividiert, erweitert man mit der konjugiert komplexen Zahl. Es ist nämlich (a + b·i)·(a − b·i) = a² + b², also eine reelle Zahl.

Beispiel:

Die Gaußsche Zahlenebene

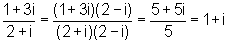
Man kann komplexe Zahlen auch in einem rechtwinkeligen Koordinatensystem darstellen. Die erste Achse ist die reelle, die zweite die imaginäre Achse. Die Zahl z = a + b·i entspricht dem Punkt (a/b) bzw. dem dazugehörigen Ortsvektor.

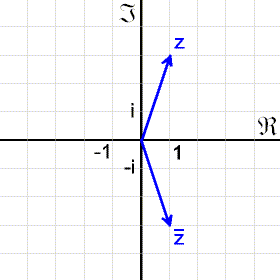
Konjugiert komplexe Zahlen liegen symmetrisch zur reellen Achse.

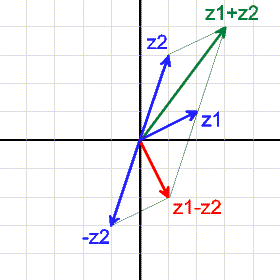
Addition und Subtraktion entsprechen der üblichen Vektoraddition und -subtraktion.

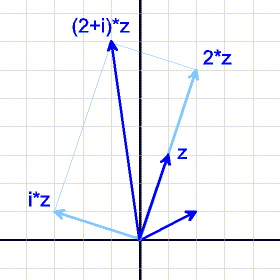
Eine Multiplikation mit einer reellen Zahl ist eine Streckung, Multiplikation mit i ergibt eine Drehung um 90°.

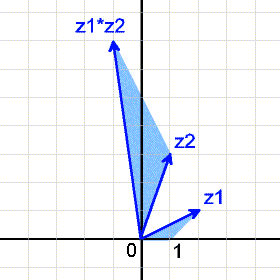
Die Dreiecke O1Z₁ und OZ₂(Z₁·Z₂) sind zueinander ähnlich.

Die Polardarstellung komplexer Zahlen

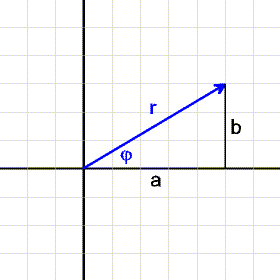
Man kann eine komplexe Zahl auch durch ihren Betrag |z| (Abstand vom Nullpunkt) und ihr Argument φ (Winkel, den sie mit der x-Achse einschließt) angeben:

Wir können daher auch schreiben: z = r·(cos(φ) + i·sin(φ)) oder kürzer z = (r; φ).

(Man vereinbart meist, dass φ zwischen 0° und 360° liegen soll. Weil die Umkehrung der Tangensfunktion nicht eindeutig ist, sollte man bei der Berechnung von φ immer eine Skizze machen!)

Die Multiplikation und Division von komplexen Zahlen ist in der Polardarstellung ziemlich einfach. Die Multiplikation mit (r; φ) entspricht nämlich einer Streckung um den Faktor r mit einer gleichzeitigen Drehung um den Winkel φ. Mit anderen Worten: wenn man zwei komplexe Zahlen multipliziert, werden die Beträge multipliziert und die Winkel addiert; bei einer Division werden die Beträge dividiert und die Winkel subtrahiert.

(r₁; φ₁)·(r₂; φ₂) = (r₁·r₂; φ₁ + φ₂)

(r; φ)ⁿ = (rⁿ; n·φ)

Die letzte Gleichung schreibt man oft in anderer Form (Formel von de Moivre):

[r·(cos(φ) + i·sin(φ))]ⁿ = rⁿ·(cos(n·φ) + i·sin(n·φ))

Die Regeln für das Wurzelziehen sind analog, aber Achtung:
Wenn man zum Argument einer komplexen Zahl ein Vielfaches von 360° addiert, ändert sich die Zahl nicht.
Wenn man zum Argument von z ein Vielfaches von 360°/n addiert, ändert sich zⁿ nicht.
Fürⁿ√z gibt es daher n verschiedene Möglichkeiten:

      (k = 0, 1, ..., n−1)

Die komplexe Exponentialfunktion

Im Reellen gilt: e^x = lim_n→∞(1 + x/n)ⁿ. Diese Gleichung können wir auch zur Definition von e^z für komplexe z verwenden.

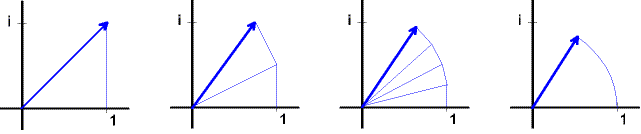
Die ersten drei Bilder zeigen 1 + i, (1 + i/2)² und (1 + i/4)⁴. Wie man sieht, nähert sich der Streckenzug immer mehr einem Kreisbogen der Länge 1 an (viertes Bild). Es ist also eⁱ = cos(1) + i·sin(1). (Der Winkel ist dabei im Bogenmaß angegeben!) Man kann zeigen, dass allgemein die Euler'sche Formel gilt:

e^i·φ = cos(φ) + i·sin(φ)       (φ im Bogenmaß)

Die Polardarstellung einer komplexen Zahl wird daher zu z = r·e^i·φ.
Setzt man φ = π (= 180°), so erhält man die bemerkenswerte Gleichung

e^i·π = −1

Ausführliche Erklärungen:
Lernpfad "Komplexe Zahlen" von Andreas Pester: http://www.mathe-online.at/lernpfade/complex/
Dave's Short Course on Complex Numbers (englisch): http://www.clarku.edu/~djoyce/complex/

Übungen

Geschichte der komplexen Zahlen

Eine Anwendung der komplexen Zahlen: Komplexe Wechselstromrechnung